Despite the rapid proliferation of digital electronics, the world is still thickly populated with analog gadgets, and the evolution of these machines is closely linked with the invention of the computer. For hundreds of years, historians believed that the great French mathematician and philosopher Blaise Pascal invented the first mechanical calculator in approximately 1642. Pascal’s machine was a small metal box equipped with a set of interlocking metal gears; by turning the numbered dials on the outside of the box, you could add and subtract. As it turns out, however, the first calculator wasn’t invented by Pascal but by an obscure German professor named Wilhelm Schickard. Schickard’s calculator was built in 1623 – the year Pascal was born. This fortuitous discovery was made in 1935 by an alert German historian by the name of Franz Hammer, and it led to the reconstruction of Schickard’s machine and to the historical resurrection of its inventor.

Schickard was born in Herrenberg, a small town near Stuttgart, in southwestern Germany, on 22 April 1592. Not much is known about him. His father, Lukas, was a carpenter; his mother, Margaret, the daughter of a Lutheran minister. A precocious child, he won a scholarship to a monastery school in the nearby town of Tubingen. (The scholarship was awarded by the government of Württemberg, then a quasi-independent state.) After graduating from the monastery, he entered the seminary at the University of Tubingen, where he studied theology and prepared for the ministry. He received a B.A. in 1609 and, two years later, an M.A. In addition to theology, he specialized in what were then known as the Oriental languages – Arabic, Hebrew, Persian, and Syrian. From 1613 to 1619, he served as a pastor or deacon in several nearby towns, and then returned to his alma mater as a professor of Hebrew and Oriental languages.

Schickard was a polymath, with a wonderful talent for languages. He was also a skilled mechanic, cartographer, and engraver whose published writings span an extraordinarily wide range of subjects – mathematics, astronomy, optics, meteorology, cartography, Semitic studies, and theology. Even at a time when the extent of knowledge in any field was considerably smaller than it is today, and a determined individual could master several diverse disciplines, the range and variety of Schickard’s achievements are impressive. He was a universal man – the first of many in the history of computers – with a rare mixture of scientific and artistic ability.

In the winter of 1617, Schickard met Johannes Kepler, the great mathematician and astronomer. Kepler was passing through Tubingen on his way to Leonberg, the Württemberg town where his mother had been accused of being a witch. The old woman, whom the mathematician had once described as “thin, garrulous, and bad-tempered,” faced torture and trial (in that order), and Kepler was on his way to Leonberg to arrange for her defense and eventual acquittal. Imperial mathematician to the Holy Roman Emperor, Kepler was a famous and controversial man, much persecuted for his religious beliefs; he was a Lutheran with strong Calvinist leanings, and his faith ran counter to the prevailing dogma. Ironically, his religious stand caused him infinitely greater grief than his revolutionary scientific achievements, which most people didn’t understand and, therefore, were less well known.

It is believed that Michael Maestlin, an astronomy professor at the university, introduced Schickard to Kepler. Although Kepler was twenty-four years older than Schickard, the two men had much in common, professionally and personally – the same religion, the same alma mater, the same home province, the same scientific interests – and they became friends. Their relationship speaks well of Schickard, who was only a twenty-five-year-old deacon at the time, not only because the great Kepler was interested in him but because Schickard himself was willing to risk the general disgrace that surrounded a man whose family had been touched by the devil and whose religious beliefs contradicted the church’s. Kepler was impressed with the multitalented Schickard and later asked him to draw the tables of figures for his great work, Harmonice Mundi (World Harmony, 1619). The two men corresponded with each other for several years, and Schickard looked after Kepler’s son when the young man attended the University of Tubingen. (And he took over Maestlin’s chair when the professor died in 1631.)

In their letters and conversations, Schickard and Kepler discussed the latest mathematical and scientific achievements, including logarithms and Napier’s rods. Schickard’s calculator appears to have been an outgrowth of these discussions, although it seems that he conceived of the machine on his own. In any event, Schickard, who liked to work with his hands, designed and built the Calculating Clock, as he called his invention, sometime in 1623.

On 20 September 1623, Schickard wrote Kepler a letter that described, in Latin, the result of his labors. “What you have done in a logistical way (i.e., by calculation),” Schickard announced,

I have just tried to do by way of mechanics. I have constructed a machine consisting of eleven complete and six incomplete (actually “mutilated”) sprocket wheels which can calculate. You would burst out laughing if you were present to see how it carries by itself from one column of tens to the next or borrows from them during subtraction.

Schickard’s next letter, written on 25 February 1624, brought bad news:

I had placed an order with a local man, Johann Pfister, for the construction of a machine for you; but when half finished, this machine, together with some other things of mine, especially several metal plates, fell victim to a fire which broke out unseen during the night. … I take the loss very hard, now especially, since there is no time now to produce a replacement soon.

At this point, the Calculating Clock disappears into the sands of time. In 1618, the Thirty Years’ War erupted in Prague, and half of Europe was swept up into the madness. For three decades, the armies of Germany, Austria, Sweden, France, and Spain marched to and fro across the Continent. The majority of the soldiers were mercenaries with a professional interest in prolonging the war; they ravaged the countryside for food and plunder, and left ruin, starvation, and disease in their wake. Germany, the main battleground, lost about 40 percent of its population, mostly through starvation and plague; in some regions, such as Württemberg, which the war reached in the late 1620s, more than half the populace perished. Schickard died of bubonic plague on 24 October 1635, and his family passed away at about the same time. In all likelihood, his house and possessions were burned, looted, or given away.

With the death of Schickard’s family, no one was left to memorialize his achievements. Aside from an occasional reference in obscure sources, the Calculating Clock was forgotten. But, against all odds, some of Schickard’s papers were preserved in the Stuttgart Landesbibliothek and the two letters quoted above wound up in collections of the astronomer’s works. The first letter was included in a collection of Kepler’s papers that came to rest in the Pulkovo Astronomical Observatory outside Leningrad, while the second was published in a volume of Kepler’s works entitled Litterae ad Kepplerum (1718). (Catherine II of Russia acquired most of the astronomer’s manuscripts, bound in eighteen volumes, in 1773.) Unfortunately, the many scientists, historians, and archivists who pored over Kepler’s literary remains failed to recognize the importance of Schickard’s letters, which is quite understandable given the size of Kepler’s papers. And there wasn’t much reason to pay any attention to the dusty Schickard material in Stuttgart.

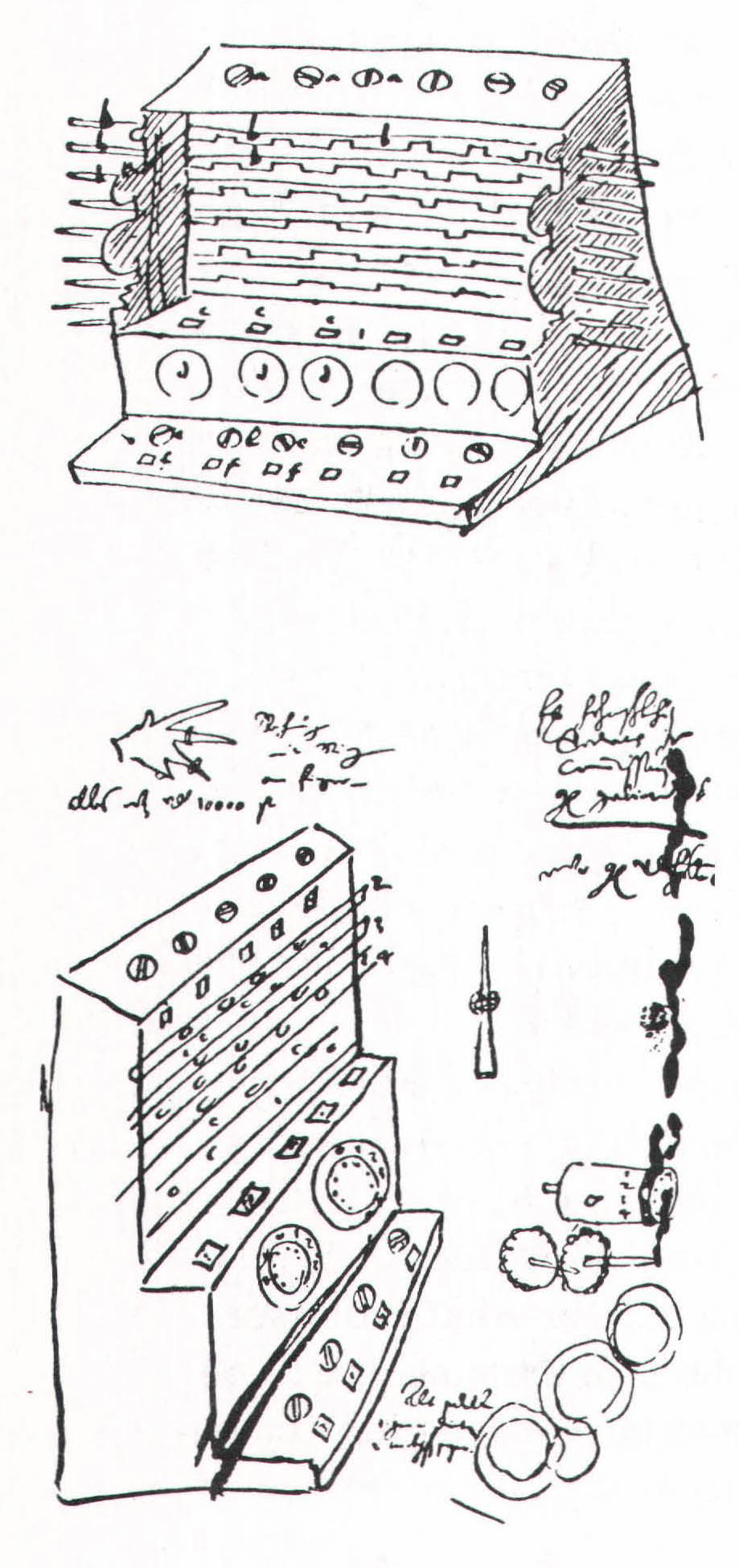
In the early 1930s, the German Research Union and the Bavarian Academy of Sciences decided to publish a complete edition of Kepler’s works. Max Caspar, Kepler’s noted biographer, and Franz Hammer, another Kepler expert, were the co-editors of the series. One day in 1935 Hammer was sifting through copies of the astronomer’s papers at the Pulkovo Observatory when he came across a curious slip of paper about the size of a postcard. The paper contained a rough drawing of a gadget of some sort. In the letter to Kepler published in Litterae ad Kepplerum, Schickard describes his invention in detail and refers to an enclosed sketch, but the drawing had been lost. Fortunately, Hammer remembered that letter, and linked the drawing to it. Although he realized that he had found documentary evidence of the invention of a mechanical calculator, Hammer, burdened with a great deal of work and hampered by the outbreak of World War II, didn’t publicize his discovery.

Twenty-one years later, Hammer was examining Schickard’s papers in Stuttgart when, as luck would have it, he found another drawing of the calculator along with a small piece of paper containing instructions for a mechanic. The drawing jarred his memory, and he decided to announce his findings. In 1957, at a Congress on the History of Mathematics at a mathematical institute in Oberwolftach, in the Black Forest, he presented what he had found. One of the people in the audience was Dr. Bruno Baron von Freytag Loringhoff, a mathematics professor at the University of Tubingen and, in a manner of speaking, Schickard’s spiritual descendant. Since Hammer didn’t understand how Schickard’s device worked, Professor von Freytag, who knew a bit about old mathematical methods, studied Schickard’s documents and deciphered the puzzle. Back in Tubingen, Professor von Freytag embarked upon the reconstruction of the machine, and completed a working version in 1960.

Schickard’s calculator, which resembles a mechanical cash register, was actually two machines in one; the top half was simply a version of Napier ‘s logs, minus the oblique line, laid out on six cylinders suspended in a wooden box. The face of the box was composed of nine wooden slats with little windows cut out of the slats to show the numbers on the rods. If, for example, you wanted to multiply 332 by 5, you turned the first three rods to 332, slid the fifth slat to the left, and added the products that appeared in the windows of that slat. As long as the multiplications were simple enough, you could get the final result by toting up the numbers on the logs in your head. But if your multiplier had several digits, you were better off entering the product of each multiplier on the mechanical adder that Schickard installed in the bottom of the machine, underneath the rods.

There are six numbered dials on the face of that adding and subtracting mechanism. Those dials are connected to six axles in a box behind them. The chief technical problem in building a mechanical calculator is the design of a device for carrying or borrowing tens, and Schickard apparently solved the problem by equipping each of the axles with a single-toothed gear. (These are the mutilated gears mentioned in his letter.) Each single-toothed gear was linked to an intermediate gear, which in turn meshed with a gear on the adjacent axle. When, for example, you turned the first numbered dial past zero, the single-toothed gear nudged the intermediate one, which moved the adjacent axle a notch. As a result, a ten was added to that axle’s numbered dial. (Much the same way automobile odometers work.) Subtraction was accomplished by turning the dials in the opposite direction, and all the results showed up in little windows above the dials.

With typical German thoroughness, Schickard outfitted the base of the machine (directly under the adding and subtracting mechanism) with six independent numbered wheels, which enabled the user to store a number while he or she fiddled with the rods or adding dials. And he installed a bell, or what Professor von Freytag believes may have been a bell, in the machine to notify the user when an addition or subtraction exceeded the calculator’s capacity; the bell was rung whenever the sixth main gear attempted to carry a ten forward or backward. Despite its numerical limitations, the machine (or Professor von Freytag’s reconstruction) worked quite well. Schickard had created the mathematical equivalent of the wheel, but his invention, swallowed up by the Thirty Years’ War, had no effect on the technology of mechanical calculation.

Back                                                                                                                                   Continue