By the mid-1930s, in part as a result of the success of the differential analyzer, a handful of scientists and engineers in the United States, Great Britain, and Germany began to give serious thought to the mathematical potential of machines. These men worked alone or in small teams and had little or no contact with each other, although they sometimes wrote about their efforts or discussed their ideas at scientific and engineering conferences. Babbage’s Analytical Engine, with its wonderfully simple but highly flexible structure of mill, store, control, and card readers, had been almost completely forgotten, except in Britain, and its underlying principles had to be rediscovered. The first man to do so was a young German engineer named Konrad Zuse.

As an engineering student at the Technical College of Berlin- Charlottenberg, in Berlin, Zuse had to master the theory of static indeterminate structures, which is based on a branch of algebra known as linear equations. Mathematically, linear equations are the flip side of differential equations; whereas the latter describe the behavior of dynamic entities, like projectiles, the former deal with the behavior of static structures, like buildings. For example, in order to provide the proper structural support for a roof, an engineer must first solve a set of simultaneous linear equations that takes into account all the relevant variables, such as the weight, strength, and elasticity of the construction materials. While these formulae are not especially intellectually profound, they were maddeningly difficult in Zuse’s day; the practical limit for an individual was about six equations with six unknowns, and a doubling in the number of equations creates an eightfold boost in the quantity of calculations. Even with the help of automatic calculators, a team of engineers needed months to solve the equations related to a big roof.
Surely, thought Zuse, there must be a better way. It was 1934, and he was still in school. He hated the mathematical drudgery of his profession and didn’t relish the prospect of a career spent hunched over a desk, figuring out equations, linear or otherwise. Although he wasn’t much of a mathematician, he knew a lot about mechanical engineering – enough to know that another mechanical calculator, full of oily gears and axles, wasn’t the answer. Fortunately, he was blessed with a good deal of insight and common sense, and his approach was fresh and original, unfettered by tradition and the opinion of experts. After carefully considering the nature of the problems of mechanical calculation, he made three conceptual decisions that put him on the right track from the beginning.
First, he decided that the only effective solution to the computational obstacles of his profession was a universal calculator, one that could solve any equation. Therefore, he provided his machine with a marvelously simple but highly flexible internal structure – the same structure Babbage had given the Analytical Engine. (However, Zuse didn’t learn about the Englishman until 1939.) The calculator was equipped with an arithmetic unit (or central processing unit) for performing the computations; a memory for storing the numbers; a control unit for supervising the flow of numbers and instructions within the machine; a so-called program unit for reading instructions and data from punched tape; and an output unit for displaying the results.
Second, Zuse decided to use binary, rather than decimal, math – a decision that was pure inspiration and ensured his success. The irreducible economy of the binary system meant that the calculator’s components could be as simple as on/off switches and that, in the final analysis, his machine was really a miniature telegraph system, with a vocabulary of zeros and ones instead of dots and dashes. Although Western mathematicians had known about binary math since Leibniz’s time, Zuse was the first one to use it in a calculator; for hundreds of years, the decimal system was regarded as a God-given sine qua non until Zuse (and other inventors, unaware of Zuse’s work) questioned the unquestionable. Even Babbage, who had considered using other number systems in the Analytical Engine, had come down on the side of tradition, primarily because gears were ideally suited to decimal math.

Finally, Zuse devised a simple set of operating rules to govern the machine’s internal operations. Although he didn’t realize it at the time, these rules were simply a restatement, in his own notation, of the basic axioms of Boolean algebra (or Boolean logic), and they enabled him to harness his machine’s binary components to useful ends. Boolean algebra, named after the English mathematician George Boole (1815-64), is a system of symbols and procedural rules for performing certain operations on numbers, letters, pictures, objects – whatever. (Leibniz inaugurated the search for such a system in his De Art e Combinatoria.) While this form of algebra may seem forbiddingly abstract, it’s really not much more complicated than ordinary arithmetic. For example, just as the appearance of a times sign (x) between two numbers calls for a multiplication, the appearance of a Boolean symbol between two numbers, letters, or statements, also calls for the performance of a specified operation.
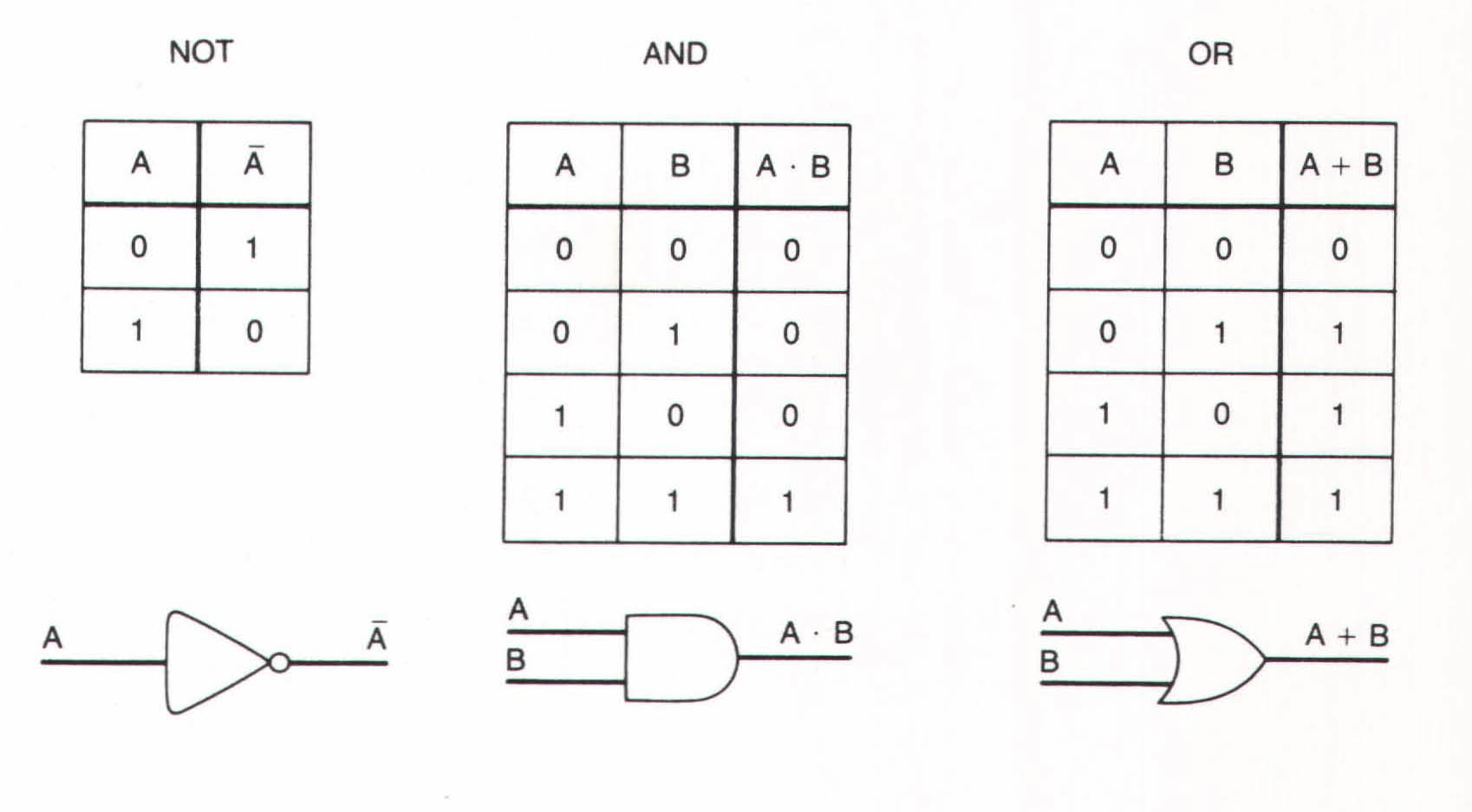
There are many operations in Boolean algebra but the three most basic are called AND, OR, and NOT. They are binary in nature, able to process only two different kinds of entities, and they, along with other Boolean operations, are often called gates, an apt metaphor for their functions. (Although Boole’s system may be applied to any group of items, we’ll confine our examples to binary numbers.) AND is a gate for 1s; if both numbers trying to slip through an AND gate are 1, AND requires the passing on of a single 1 to the next gate up the road. But any other combination of digits (two 0s or a 1 and a 0) will yield a 0. OR is a less selective sieve for 1s; if either of the numbers at its gates is 1, then OR will pass on a 1. As for NOT, it acts as an inverter, transforming any 1s or 0s that come knocking on its door into their opposites (a 1 into a 0 and vice versa).
Although Boolean algebra contains other operations, AND, OR, and NOT are all you – or a machine – need to add, subtract, multiply, divide, and perform other logical processes, such as comparing numbers or symbols. Given the binary character of Boolean gates, it’s a relatively easy matter to engineer a binary calculator’s components into patterns that mimic AND, OR, and NOT. Of course, nothing could have been further from Boole’s mind than the idea of incorporating his system into a machine; yet the invention of the computer owes almost as much to Boole, a self-taught mathematician who never went to college, as to anyone else.
In two epochal works, The Mathematical Analysis of Logic – Being an Essay Towards a Calculus of Deductive Reasoning (1847) and An Investigation of the Laws of Thought (1854), Boole sought to identify the procedural rules of reasoning and to establish a rigorous system of logical analysis. Before the publication of these works, formal logic was a sleepy discipline with little to show for thousands of years of efforts. Its most powerful analytical tool was the syllogism, a form of deductive reasoning that proceeds from a major to a minor premise and then to a conclusion, as in “All men are mortal; all heroes are men; therefore all heroes are mortal” – not much to crow about. One of the most important results of Boole’s work was the demise of logic as a philosophical discipline and its rebirth as a vigorous branch of mathematics.

Although most logicians criticized or ignored Boole’s ideas, they were absorbed by a growing number of mathematicians, who refined and amplified them, and Boole was rewarded with a professorship at Queen’s College, in Ireland. (Babbage, who knew a good idea when he saw one, wrote in the margin of his copy of The Mathematical Analysis of Logic, “This is the work of a real thinker.”) And then, in 1910, the British logicians Alfred North Whitehead and Bertrand Russell published the first installment of their three-volume Principia Mathematica (1910-13), which transformed Boolean algebra into a formidable intellectual system known as symbolic logic. We’ll explore Russell and Whitehead’s ideas later in the book; for the moment, though, it’s important to remember that the internal operations of computers are governed by Boolean algebra, and that Zuse, in his uncanny instinct for the heart of the matter, was the first to incorporate these rules into a calculating machine.