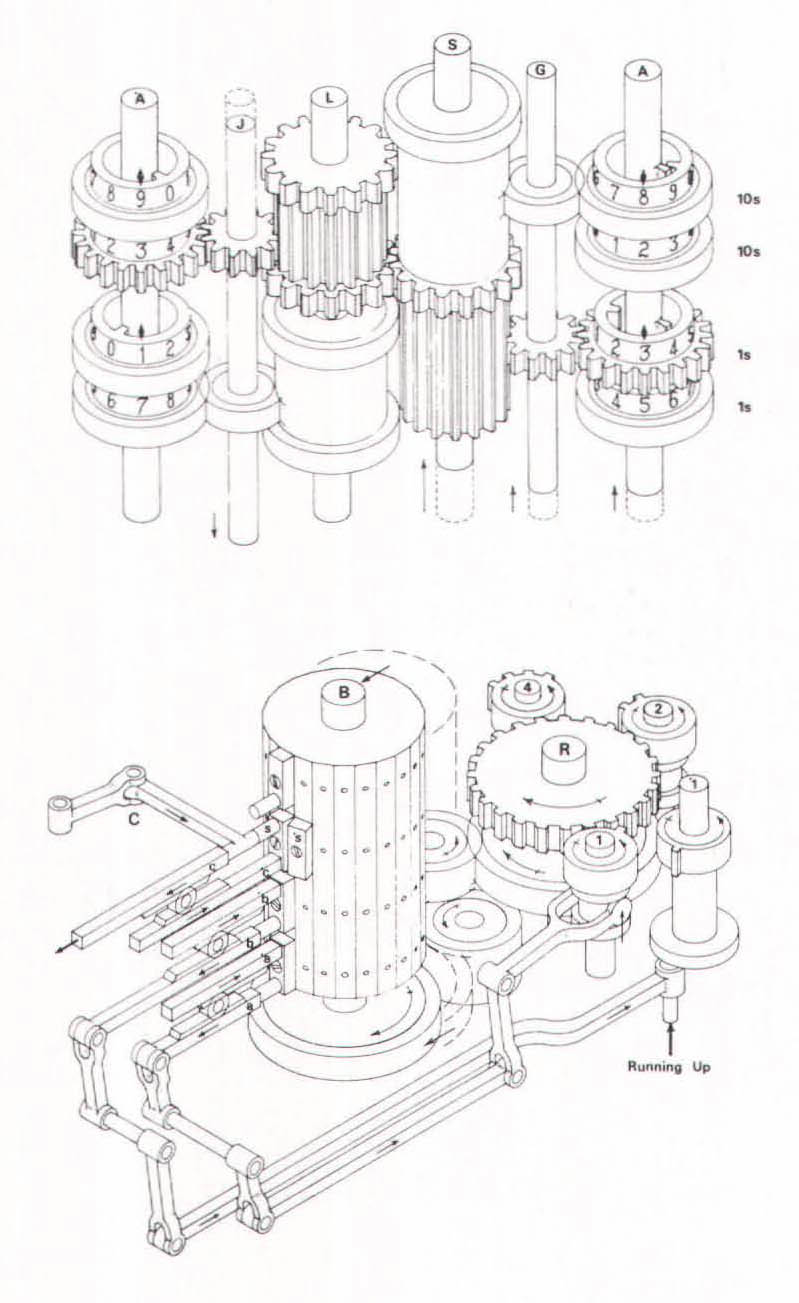
The Analytical Engine was designed in the shape of a lollipop; the stick contained the store, where the numbers were kept, and the candy held the mill, where the numbers were operated upon. (In current computer terminology, the mill was the central processing unit, or CPU, while the store was the memory.) Many times larger than the Difference Engine, the machine contained hundreds of vertical axles and thousands of wheels, or gears. The axles, which were about ten feet tall, represented a number, the wheels on the axles the digits in that number; since each axle contained forty wheels, the machine could process numbers up to forty digits long – twice the capacity of the Difference Engine. All told, the Analytical Engine would have been about fifteen feet tall and twenty-five feet long, or about as big and heavy as a small locomotive.

The mill contained nine main axles for performing multiplication and division and two accumulator axles for addition and subtraction; the accumulators also stored the results of all operations. As for the store, it held fifty primary axles and an equal quantity of adjoining secondary axles. Each of the store’s axles had two sets of wheels; since the act of reading a number from the store erased it, the extra set of wheels enabled the machine to keep a copy of the original number – meaning that the store could contain one hundred fort y-digit numbers. (And it could be enlarged by the addition of more axles.) When a number was entered into or taken out of the store, the primary axle holding the figure relayed it to the secondary axle, where it was passed on to a series of long horizontal toothed bars, or racks. Spanning the length of the store, the racks conveyed the number to an “egress axis” or an “ingress axis,” which served as gateways into and out of the store.

The machine’s internal operation was orchestrated by a barrel made up of metal slats with rectangular studs. The pattern of the studs could be varied, and each of the barrel’s fifty to one hundred slats could hold as many as four studs. (The barrel served as the control unit.) It was these studs that told the engine when and how to execute a given operation. For instance, when the engine was directed to divide a number, the barrel turned to the slat, or slats, that governed division, and slid forward, pushing the studs against a group of levers that manipulated the appropriate axles in the mill and the store. By changing barrels, the operator could alter the engine’s internal operations to suit the calculating needs of the moment.
Despite its size and complexity, the Analytical Engine was hardly a lumbering mechanical monster. The addition or subtraction of two forty-digit numbers took only three seconds, multiplication and division required two to four minutes – a pace that meant most of the calculations had to be performed by repeated addition and subtraction. Transferring a number between two adjacent axles took two and a half seconds, while a carry from the lowest wheel on an axle to the highest, or from the fortieth digit all the way through to the first, needed only a fourth of a second; Babbage, realizing that all the carrying to and fro would reduce the engine’s speed to a crawl, devised an ingenious mechanism that triggered a carry before a number wheel actually turned to nine.

The Analytical Engine’s external program was provided by punch cards – just like most of the computers of the 1950s and 1960s. Babbage got the idea of using cards from the textile industry. In 1801, the Frenchman Joseph-Marie Jacquard invented an automatic loom that was controlled by punch cards; as the cards, which were strung together into a kind of tape, moved through a mechanical reader, wooden plungers passed through the holes, orchestrating the machine’s operation. The loom’s ability was nothing less than amazing – Babbage owned a silk portrait of Jacquard sewn with instructions from about ten thousand cards – and Jacquard’s invention, which had been based on an earlier, less-efficient loom invented by another Frenchman, had revolutionized the textile business.

The Analytical Engine employed three types of cards, each with its own mechanical reader: “operation cards,” “variable cards,” and “number cards.” The first kind of card carried the instructions; the second held the symbols of the variables in an equation (x, y, and so on), the numerical value of the variables in that equation (1, 18, whatever), and certain numerical constants (like ?); and the third contained entries from mathematical tables, such as logs and trigonometric functions. This three-pronged approach was cumbersome and complicated, and the programming side of the Analytical Engine was the least-developed aspect of the machine; Babbage wrote about two-dozen programs between 1837 and 1840, but they are incomplete, segments of programs rather than entire lists of instructions.

Like a modern computer, the Analytical Engine had the ability to make decisions; that is, it could adopt one of two alternative courses of action based upon the results of its calculations. In the case of the Analytical Engine, this ability was quite limited, and the operation cards could only order the engine to add two numbers and, if the results were less than zero, to proceed to a specified card and carry out the indicated instruction (such as “add 10”). Known as a conditional jump, or branching, this is one of the most important attributes of a computer – one of the characteristics that distinguishes it from an ordinary calculator. The operation cards could also instruct the machine to repeat a given set of instructions any number of times or to perform a sidestep within a general program; both of these tricks are important programming tools, the latter called a subroutine, the former a loop.

Much of what we know about the engine’s programming potential comes from a remarkable article written by Augusta Ada Byron, countess of Lovelace, the daughter of Lord Byron, the poet. A talented amateur mathematician, Ada met Babbage in 1833 and was enthralled by the man and his work; at the suggestion of a mutual friend, she translated an article on the Analytical Engine written by an Italian mathematician. Ada added many pages of explanatory notes and her translation, published in a popular scientific journal, became the most widely circulated account of the Analytical Engine, an astute analysis of the machine and of Babbage’s ideas. Ada had a good deal of literary talent, and her notes are often quoted today: “We may say most aptly that the Analytical Engine weaves algebraic patterns just as the Jacquard-loom weaves flowers and leaves.”
Was the Analytical Engine a computer? Obviously, the answer is a matter of definition. What is a computer? What is a calculator? Unfortunately, the words are almost impossible to define. Their meanings have changed over the years, and undoubtedly will continue to change. For centuries, computer designated a person who did calculations for a living; nowadays, it applies to a certain kind of machine with a broad range of attributes and capabilities; many years from now, it may refer to a device with substantially different characteristics and applications than today’s computers. The same holds true for calculator, which was often employed as a synonym for computer. Since the late nineteenth century, calculator has referred to a small machine that people use to perform arithmetic; but it took on a much grander meaning in the 1940s, when it was enlisted to describe such “giant brains” as the Selective Sequence Electronic Calculator.
In its broadest sense, and in the modern meaning of the term, a computer is an information-processing machine. It can store data – numbers, letters, pictures, or symbols – and manipulate that data according to programs that also have been stored in the machine. The ability to retain data and programs gives computers a considerable degree of automaticity, and, equally important, the capacity to make decisions, such as the conditional jump, based on the results of its own computations. A calculator, on the other hand, can’t do any of these things. It can only solve mathematical problems, and its operation must be directed every step of the way by the user. Unable to store data and programs, it cannot make decisions. Physically, calculators vary a great deal (as we shall see), but computers generally possess five basic parts – a structure that seems to have arisen more out of practicality than tradition (just as cars have four wheels). Those parts are a central processor, a central control, a memory, and input and output units.
On the one hand, the Analytical Engine resembled a calculator. It could only perform mathematical work and could not store programs. On the other hand, it also resembled a computer. It was programmable, and possessed a large degree of automaticity and a modest ability to make decisions. And it had a memory (a store), a central processor (a mill), and a control (the barrel). Neither fish nor fowl, it was a rudimentary form of computer known as a program-controlled calculator. Such a machine falls short of being a computer in at least one all-important respect: it cannot retain a program, and its instructions are forever frozen on punch cards, tape, or another medium. Although the Analytical Engine is as far removed from a computer as an open-air biplane is from a Boeing 747, it was a great, if unrealized, intellectual achievement – a magnificent glimpse of the future.