
In 1614, John Napier (1550-1617), baron of Merchiston, Scotland, published one of the most important papers in the history of science. A highly original mathematician, Napier announced the invention of logarithms, or logs – a series of numbers that enabled multiplication and division, the two most difficult arithmetic operations, to be reduced to addition and subtraction. Instead of multiplying or dividing natural numbers (1, 2, 3, etc.) on paper or in your head, you simply looked up the numbers in a table of logs and added or subtracted the given figures; then, to get the final answer, you converted the sum of the logs back to a natural number by referring to a table of antilogs. The principle of logs is quite simple, and is based upon the fact , now taught to schoolchildren everywhere, that numerical powers can be added or subtracted: X2 x X4 = X6 or X6 ÷ X2 = X4.
In their original version, Napier’s logs weren’t useful for ordinary figuring, so Henry Briggs (1561-1630), a geometry professor at Gresham College, London, took up the grueling job of calculating the logs for thousands of natural numbers. In 1617, Briggs published a small table giving the logs for the numbers from 1 to 1,000 and, seven years later, a much larger one for 2,000 to 29,000 and 90,000 to 100,000. At a time when most people had trouble with basic arithmetic, Brigg’s tables were a mathematical godsend and were circulated widely. Other mathematicians gradually filled in the gaps in his tables, providing, for example, the logs for frequently used mathematical functions, such as sine and tangent, which made Napier’s invention an increasingly indispensable tool for navigators and surveyors.
The creation of logs was one of the seminal achievements in the history of mathematics, with a great deal of influence on the development of computers. Aside from its many practical applications, the invention led mathematicians to take a closer look at numerical powers, and the development of exponents was one result. Unlike most great scientific discoveries, Napier’s work wasn’t preceded by decades of lesser labors along the same lines by other mathematicians, and there isn’t even a hint in earlier mathematical writings of the feasibility of abbreviating such basic operations as multiplication and division. The invention was entirely Napier’s doing, the work of a determined genius in out-of-the-way Scotland, a rather primitive place compared to London, Paris, and the other intellectual centers of seventeenth-century Europe.

The wealthy lord of a castle outside Edinburgh, Napier regarded mathematics as a hobby. He attended Cambridge University for a few years but, apparently at the suggestion of an uncle who didn’t think much of English schools, finished his education on the Continent, probably at the University of Paris. Living in a time of intense religious strife – the Protestant Reformation was underway – Napier, who did not seem to do anything halfheartedly, got caught up in the general fanaticism. He became a zealous anti-Catholic, a leader in the campaign against Popism, and spent five years writing a long religious tract called Plaine Discovery of the whole Revelation of Saint John, which he composed in English instead of Latin so that “hereby the simple of this Iland may be instructed” in the Protestant way. With the peculiar shortsightedness of the zealot, Napier was certain that he would be remembered above all else for his Plaine Discovery.
Napier was also a resourceful inventor, especially in defense of God and country. He devised a large hydraulic screw for draining flooded coal mines and a small arsenal of weapons for Scotland’s defense against an anticipated invasion by the dreaded King Philip of Spain, a Catholic. (And he described these weapons in a curious document entitled Secrett Inventionis, proffitabill and necessary in theis dayes for defence of this land, and withstanding of strangers, enemies of God’s truth and religion.) He drew up plans for mirrors that could set fire to ships at a distance; a cannon that could rain shot in a circle; and a round metal chariot – a forerunner of the tank – that could carry musketeers. According to a witness, the cannon was particularly fearful, destroying several sheep and cattle (of the Catholic faith, no doubt) in a test on a plain outside Edinburgh.
In his autobiography, William Lilly, a seventeenth-century astrologer, relates an amusing story, possibly apocryphal, about the first meeting of Napier and Briggs. Lilly apparently heard the tale from a witness, John Marr:
When Merchiston [Napier] first published his Logarithms Mr. Briggs … was so surprised with admiration of them that he could have no quietness in himself until he had seen that noble person whose only invention they were. He acquaints John Marr therewith who went into Scotland before Mr. Briggs purposely to be there when these two so learned persons should meet. Mr. Briggs appoints a certain day when to meet at Edinburgh; but, failing thereof, Merchiston was fearful he would not come. It happened one day as John Marr and the Lord Napier were speaking of Mr. Briggs, “Oh! John,” saith Merchiston, “Mr. Briggs will not come now”; at the very instant one knocks at the gate, John Marr hasted down and it proved to be Mr. Briggs to his great contentment. He brings Mr. Briggs into my Lord’s chamber, where almost one quarter of an hour was spent, each beholding the other with admiration, before one word was spoken.

In the last years of his life, Napier developed another ingenious arithmetic trick – hardly as significant as logs but rather a clever little gimmick. Employing an ancient numerical scheme known as the Arabian lattice, he laid out a special version of the multiplication tables on a set of four-sided wooden rods; there was a rod, or numbered stick, for each of the ten digits, including zero. Napier’s rods, or bones, as they came to be called, were essentially a multiplication table cut up into movable columns. For example, to multiply 1,952 by 4, you picked up the rods numbered 1, 9, 5, and 2, and placed them on a wooden board outfitted with a vertical index labeled from 1 to 9. You moved your eye down to index number 4, and added up the two numbers, or partial products, that appeared in the fourth row of each of the rods. That was your answer. By repeating these operations, you could multiply and divide large numbers and find square and cube roots.
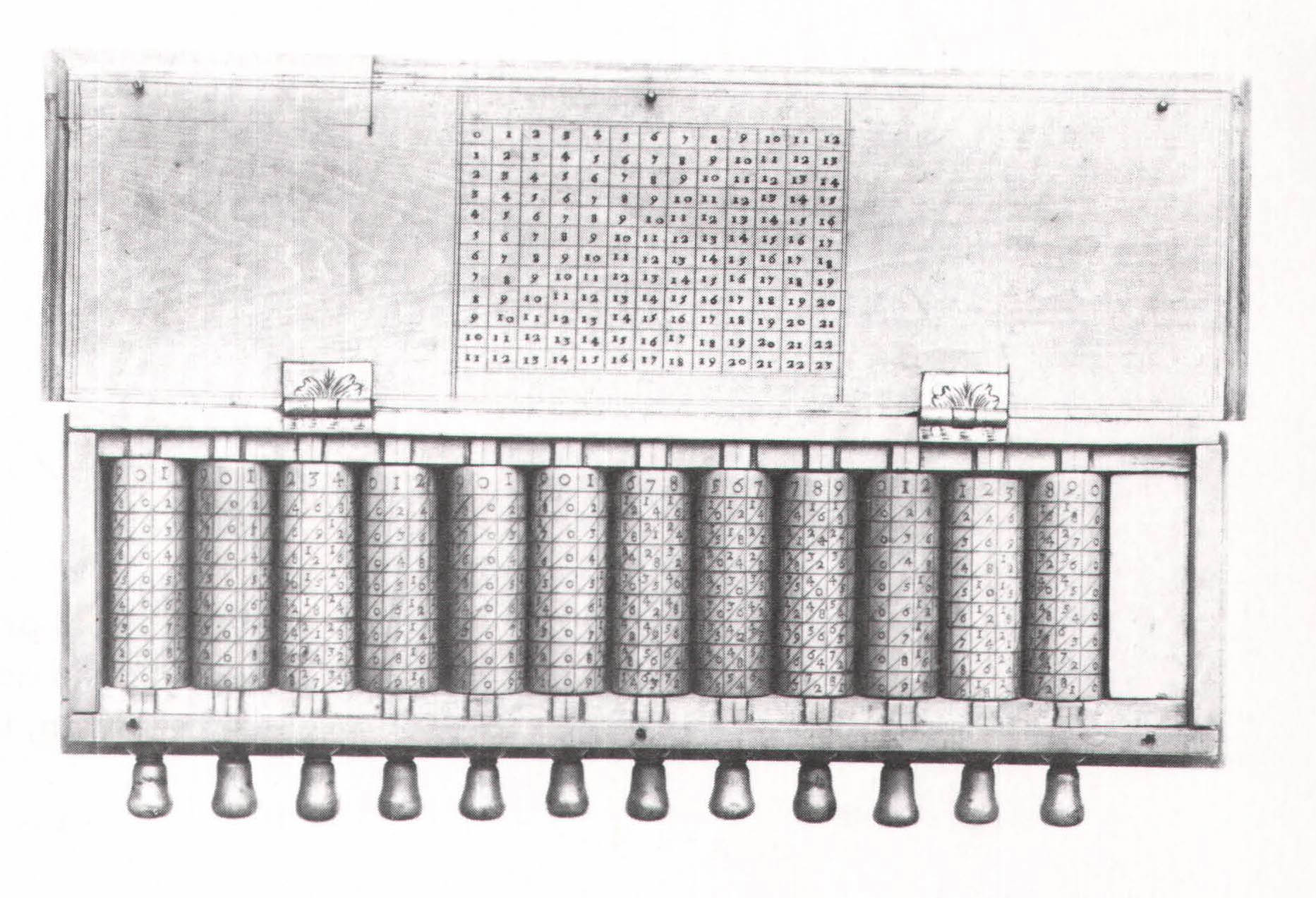
Napier’s rods were enormously popular and constituted the Scotsman’s chief claim to fame among his contemporaries. They were used all over Europe, testimony to the poor state of numeracy at the time, when even the lower rungs of the multiplication table taxed the ability of well-educated people. (Arithmetic ordinarily wasn’t taught in school.) The rods were available in basic, middling, and deluxe versions; in an especially fancy edition, they might be carved out of ivory and set in a carrying case made out of fine leather, with an addition table, pasted to the lid, thrown in for good measure. In later versions, the rods were turned into cylinders and mounted inside wooden boxes; instead of laying out the rods on an index board (to set up the multiplicand), you simply rotated them in their places in the box. In any event, Napier’s rods fell out of fashion after several decades, as people gradually got the hang of Hindu-Arabic math.