
In the eyes of the world, the first mechanical calculator was invented by Blaise Pascal. Born in 1623 in Clermont-Ferrand, in the Auvergne region of France, Blaise was the son of a well-heeled lawyer who served as the deputy president (judge) of the local tax court – a position that he had, in the tradition of the time, purchased from the government. Etienne Pascal was an intelligent man with a wide range of intellectual interests; he was especially devoted to science and mathematics and seems to have been a fairly talented mathematician. He was also a determined social climber and a loyal officer of a severely oppressive government; the France of Louis XIII and Cardinal Richelieu, the foreign minister, was rocked by savage peasant revolts, and officers of the state like Etienne occasionally were assassinated. In 1626, when Blaise was three, his mother died, and Etienne, who had become rich through quasi-official graft, resigned his judgeship and moved to Paris, where he devoted himself to the education of his son and two daughters.
Blaise’s brilliance surfaced early. As a child, he discovered several fundamental mathematical theorems (at least according to one of his sisters, whose account may be exaggerated). At sixteen, he wrote an essay on conic sections that proved a fundamental theorem about geometric shapes inscribed in conic sections. He supposedly derived four hundred corollaries from the theorem which has come to be known, in what is certainly a unique honor for a teenager, as Pascal’s mystic hexagram. (His Essai pour les coniques has been lost, but a broadside, written several years later, survived.) Most mathematicians couldn’t believe that the essay was the work of a boy; Rene Descartes, one of the seventeenth century’s most important mathematicians and philosophers, at first suspected that Etienne was the real author of the essay, and it took him a while to acknowledge Blaise’s genius.
Blaise’s short life was full of accomplishment. In his twenties, in addition to inventing a calculator and producing several mathematical treatises, he demonstrated the existence of atmospheric pressure and of vacuums. In his thirties, he invented the syringe and the hydraulic press, and enunciated the basic principle of hydraulics – a principle now known as Pascal’s law. (Briefly, it states that any pressure applied to a confined liquid will be transmitted with equal force in every direction, regardless of where the pressure is applied.) And along with Pierre de Fermat, the Swiss mathematician, he laid the foundations of the theory of probability, a project that began as a favor for a card-playing nobleman who wanted to know more about the odds of the draw. Blaise was also interested in the affairs of the world; shortly before he died, in great pain, of ulcers and stomach cancer at the age of thirty-nine, he and a group of farsighted Parisians established one of the earliest public transportation systems in Europe, a bus line in central Paris.

Blaise is one of the greatest might-have-beens in science. There’s no telling what he might have accomplished had he not died so young and had he not, at the age of thirty-two, entered a Jansenist convent outside Paris. To a large degree, Blaise’s extreme religiosity was fueled by agonizingly poor health and a pent-up sexuality – he apparently was a homosexual- and he flagellated himself for more than his share of sins. At the request of the Jansenists, Blaise generally abstained from scientific pursuits and devoted himself to the castigation of the Jesuits and the atheists. He wrote two philosophical works, Les Provinciales and the Pensees, which were considered masterpieces of expository writing and which established him as one of the founders of modern French prose.
The origin of Blaise’s calculator is rooted in both political and personal matters. In 1635, France declared war on Spain and marched into the Thirty Years’ War. Short of money, the French government reneged on part of its internal debt and stopped paying interest on certain government notes. Etienne, who had invested heavily in municipal bonds, suddenly found himself without an income. On the verge of bankruptcy, he joined four hundred investors in a tempestuous confrontation with the French chancellor, Peter Seguier, in a meeting in Paris in 1638. Richelieu was outraged by the protest and ordered the arrest of the more outspoken investors, and Etienne fled, alone, to his native Auvergne. Thanks to the intercession of influential friends and the help of one of his daughters, who charmed the cardinal with a performance in a children’s play, Etienne was restored to favor. The state needed able men like him, and he was allowed to prove his loyalty and recoup his fortune as the tax commissioner for Upper Normandy, based in the thriving port of Rouen.
At first, Etienne, who assumed his new post in 1639, was buried with work. He and his son were often up until two or three o’clock in the morning, figuring and refiguring the ever-rising tax levies with the help of counting boards. In the course of their labor, it occurred to Blaise that it might be possible to mechanize their calculations with a device that counted numbers much as a timepiece marked the passage of time. “The calculating machine,” wrote a reviewer in Le Figaro Litteruire in 1947, “was born of filial love flying to the rescue of the tax man.” With his father’s encouragement – Etienne was nothing if not forward looking – Blaise went to work designing an apparatus that could do the job. It was 1642 and Blaise was nineteen.
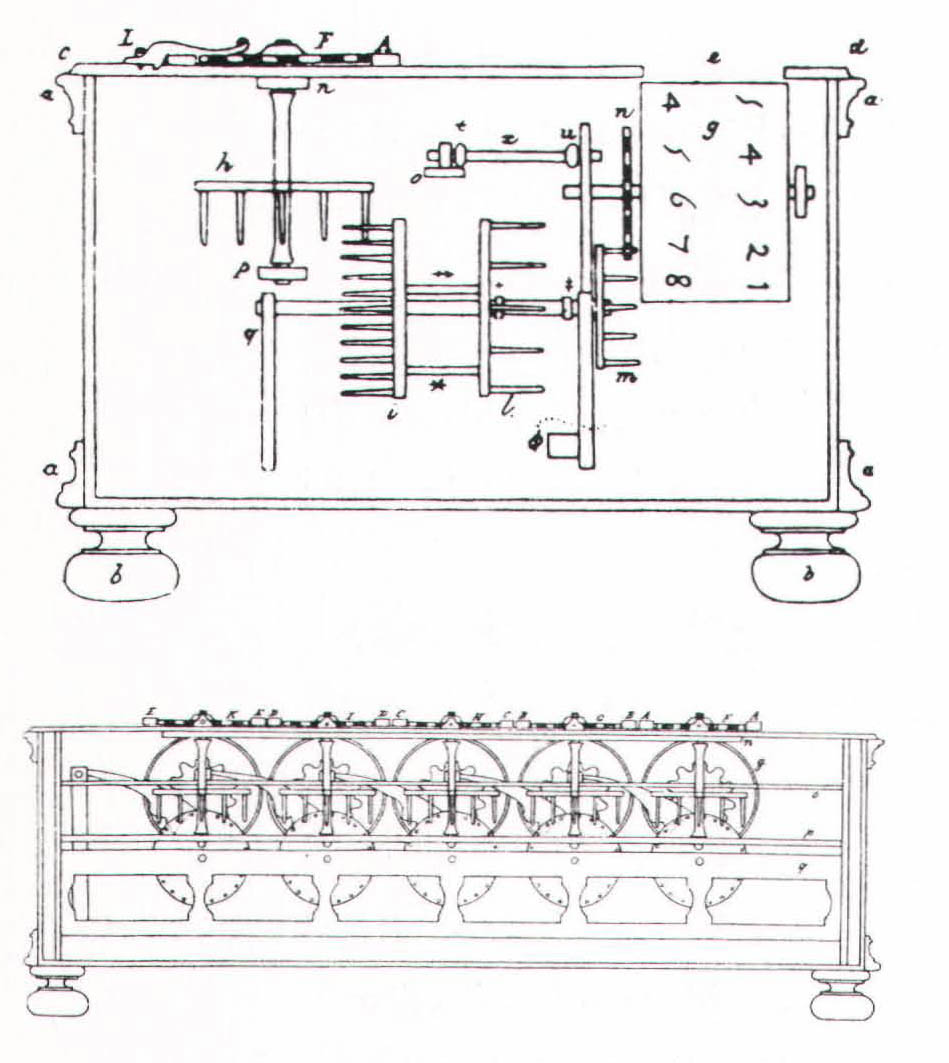
A high-strung perfectionist, he labored on the machine for two or three years, experimenting with many different designs, components, and materials. Etienne hired workmen to make prototypes under his son’s direction, but the going was slow, partly because of Blaise’s fastidiousness, partly because of the primitive state of metalworking at the time; it was very difficult to cut precisely toothed gears. Blaise finally came up with a feasible design – a five-digit calculator about the size of a shoe box, with dials on the front for entering the numbers and crown-type gears on the inside for calculating the answers, which appeared in little windows on the face. A practical engineer, he tested the solidity of the gadget by taking it on bumpy carriage rides in the country. Although the machine seemed sturdy enough, its five-digit capacity was plainly inadequate, and Blaise went on to develop six and eight-digit models.
The Pascaline or Pascale, as the elegant contraption came to be called, looked much better than it worked. It was really good only for basic addition. Addition was performed simply enough – you dialed in the numbers and the answers appeared in the little windows on the face – but subtraction was a rather tedious procedure. As Pascal designed the device, the gears could turn in one direction only – we’ll see why in a moment – which meant that subtraction had to be carried out by a roundabout method known as nines complements. An ancient trick, nines complements transforms subtraction into a form of addition. As for multiplication and division, the Pascaline accomplished them, maddeningly enough, by repeated addition and subtraction.

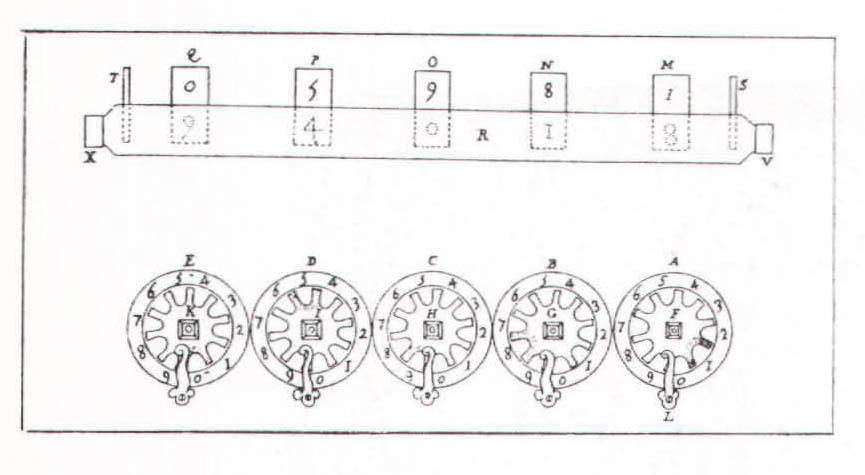
The nines complement method is worth a closer look, since it is also used in many computers. Say you wanted to subtract 600 from 800 on the Pascaline. First, you pulled down a thin horizontal slat that masked the regular answer windows. A new set of numbers was revealed on the drums – the nines complements. Then you dialed in 600, which produced a nines complement of 399, or the difference between 600 and 999. Next you returned the slat to its regular position and added 800 and 399, which gave 1199. Finally, you mentally performed an end-around carry, adding the leftmost digit in 1199, or 1, to 199, which yielded the answer, 200. A nines complements is merely the difference between a given figure and a row of nines, the size of the row being determined by the number of digits in the figure. By using nines complements, or a variant known as tens complements, a computer can perform addition and subtraction, and therefore multiplication and division, with the same circuits.

Inside, the Pascaline consisted of five to eight axles. There were three crown-type gears on each axle, with a fourth perpendicular gear linking the axles to the dials on the face of the machine. The axles also held the numbered drums. Whenever a ten was carried, a weighted ratchet between the main gears nudged the adjacent gear, or next highest power of ten, around a notch, and so on down the row. In theory, the weighted ratchets were supposed to make it easier for the Pascaline to perform carries; but, in practice, the ratchets tended to jam – the machine’s major technical drawback. Moreover, the ratchets prevented the gears from turning in more than one direction, necessitating a roundabout approach to subtraction.
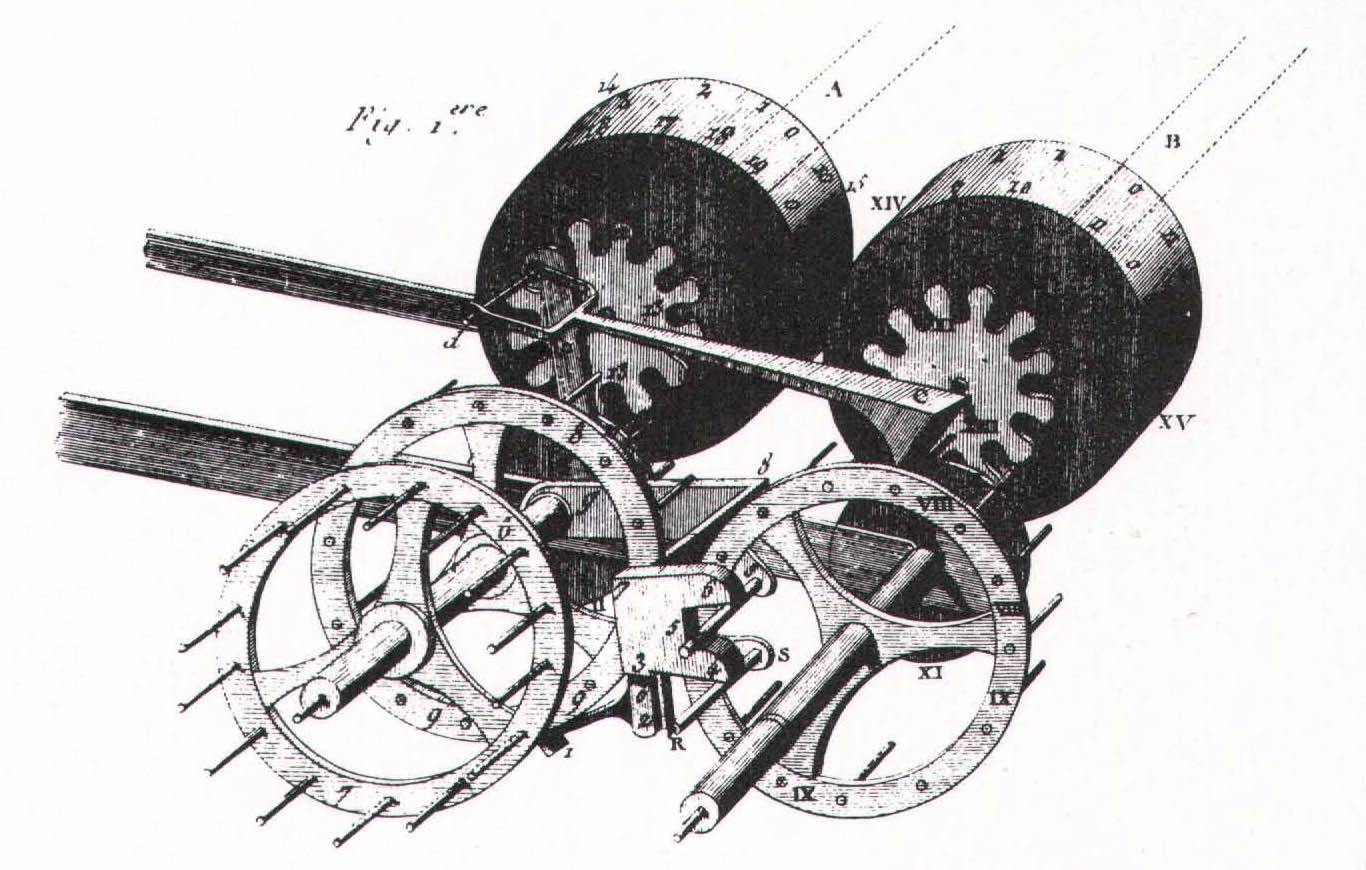
With its weighted ratchets and eight-digit capacity, the Pascaline was conceptually more ambitious than Schickard’s Calculating Clock. But the German’s six-digit machine, with its simple carrying mechanism, worked perfectly, while Pascal’s creation did not. (By the way, the clock’s capacity for multiplication and division derived from the unmechanical stratagems of Napier’s rods and any user of the Pascaline could have compensated for its multiplying and dividing deficiencies by buying a set of rods.) Nevertheless, the Pascaline was a historic achievement, for it demonstrated that an apparently intellectual process like arithmetic could be performed by a machine. (Of course, the Calculating Clock was also a cogent demonstration of the power of machines, but it had no historical impact.)
Despite its shortcomings, the Pascaline was an instant sensation. Rouen’s elite trooped through the Pascals’ drawing room for free demonstrations, and Etienne and his son took their mechanical wonder to Paris, where they showed it off to royalty, businessmen, scientists, and government officials. Pierre de Ferval, a family friend and a mathematics professor at the Royal College of France, agree d to demonstrate the contraption to prospective customers in his apartment at the College Maitre Gervais every Saturday morning and afternoon. He would sell the machine – on commission, of course – and teach buyers how to use it. Blaise went to work writing advertising flyers for the invention and asked another friend, the poet Charles Vion Dalibray, to compose a publicity sonnet:
Dear Pascal, you who understand with your subtle insight
What is most admirable in mechanics
And whose skill gives us today
A lasting proof of your marvelous genius,After your great intelligence, what is the point of having any?
Calculation was the action of a reasonable man,
And now your inimitable skill
Has given power to the slowest of wits.For this art we need neither reason nor memory
Thanks to you, each of us can do it without fame or pain
Because each of us owes you the fame and the result.Your mind is like that fertile soul
Which runs everywhere inside the world
And watches over and makes good whatever is lacking in all that is done.
Perhaps inevitably, counterfeit versions of the Pascaline appeared on the market, Blaise was furious. “I have seen with my own eyes one of these false products of my own idea,” he wrote in one of his publicity broadsides, “constructed by a workman of the City of Rouen, a clockmaker by profession . . .
After being given a simple account of my first model, which I had constructed several months previously, he was bold enough to attempt another, and what is more, with a different kind of movement; but since the fellow has no aptitude for anything except the skillful use of his own tools and does not even know whether there is such a thing as geometry or mechanics, the result was that (though very competent in his own line of business and very industrious in various ways un connected with it) he simply turned out a useless object, nice enough to look at, to be sure, with its outside smooth and well-polished, but so imperfect inside that it was no good for anything; but owing simply to its novelty it aroused a certain admiration among people who knew nothing at all about such things, and notwithstanding the fact that all the basic defects came to light when it was tested , it found a place in the collection of one of the connoisseurs of this same city which was filled with rare and interesting things. The sight of this little abortion was extremely distasteful to me and so chilled the enthusiasm with which I was working at the time to perfect my own model that I dismissed all my workmen, fully intending to abandon the enterprise owing to the fear I rightly felt that others might set to work with the same boldness and that the spurious objects they might produce from my original thought would undermine both public confidence and the use that the Public might derive from it.
Blaise applied for a patent, or privilege as it then was called, but it was slow in coming. Unluckily for him, the issuing of patents was controlled by the office of Chancellor Seguier, who had presided over the boisterous investors’ meeting of 1638. Seguier had a long memory. Although the Pascals’ had attempted to appease the chancellor by dedicating one of their first calculators to him, Seguier didn’t act on their patent application until 1649, four to five years after the Pascaline’s debut.

Patented or not, the machine failed to sell, even though there obviously was a need for it, given the poor state of numeracy in seventeenth-century France. There were several reasons for its failure, including its tendency to malfunction and its limited mathematical ability, which didn’t make it very helpful to bookkeepers, clerks, and businessmen who could have used a good adding machine. The Pascaline was also very expensive, going for 100 livres, or pounds, apiece, which was enough to keep a seventeenth- century Frenchman in modest comfort for a year. Moreover, people were suspicious of a machine that could count; if a scale or a roulette wheel can be fixed, so can a calculator, and more than two hundred years were to pass before most people could place their trust in nuts and bolts. At the very least, the Pascals expected that they’d be able to sell the machine to royalty, but the aristocrats disdained arithmetic and intellectual matters in general; bookkeeping was for servants. It’s not known how many machines were sold but the total was probably no more than ten or fifteen.